
In computer science the Big-O notation is used to describe the performance or the algorithmic complexity of an algorithm. This short post will describe some of these notations.
To demystify the simple math behind these notations we shall use straightforward Java code examples. The notations we shall explore are the following:
- O(1) – Constant Time Algorithm
- O(n) – Linear Time Algorithm
- O(n^2) – Quadratic Time Algorithm
- O(log n) – Logarithmic Time Algorithm
One method often used to evaluate the performance of an algorithm is to measure the total execution time relative to the input size. In the above case n denotes the input size while the O is the worst-case scenario growth rate function.
O(1) – Constant Time Algorithms
Describes an algorithm that will execute in the same time regardless of the size of the input. Here regardless of the array size whether there is no element in the array or there is 1 or a million element the time taken to return will be constant.
public boolean isEmpty(int[] arr) {
return arr.length == 0;
}
O(n) – Linear Time Algorithms – (Linear Search)
Describes an algorithm that will linearly increase based on the size of the of the input. The time to search increases proportionately to the number of items introduced.
public boolean containsValue(int[] arr, int val) {
for(int i : arr) {
if (i == val) {
return true;
}
}
return false;
}
O(n^2) – Quadratic Time Algorithms
Describes an algorithm whose performance is directly proportional to the square of the size of the input. Here if the array contains 2 elements then this method will print four times (22) = 4. If it contains 10 elements then it will print a hundard times (102) = 100.
public void printPairs(int[] arr) {
for (int firstItem : arr) {
for (int secondItem : arr) {
System.out.println("[" + firstItem + "," + secondItem+"]");
}
}
}
O(log n) – Logarithmic Time Algorithms – (Binary Search)
Describes an algorithm that will increase based on the size of the of the input but not proportionately. One place where you might have heard about O(log n) is in Binary search.
private int recursiveBinarySearch(int[] arr, int searchedElement, int lowIndex, int highIndex) {
int elementPos = -1;
int midIndex = (lowIndex + highIndex) / 2;
if (searchedElement == arr[midIndex]) {
return midIndex;
} else if (searchedElement < arr[midIndex]) {
recursiveSearch(arr, searchedElement, lowIndex, midIndex-1);
} else if (searchedElement > arr[midIndex]) {
recursiveSearch(arr, searchedElement, midIndex+1, highIndex);
}
return elementPos;
}
Note: the key aspect for the search algorithms is that here is that the array/list is sorted.
Sum Up
| O(1) – Constant Time | Find if a number is even or odd. Check if an item on an array is null. |
| O(n) – Linear Time | Find max element in unsorted array, Duplicate elements in array with Hash Map |
| O(n^2) – Quadratic Time | Sorting array with bubble sort |
| O(log n) – Logarithmic Time | Finding element on sorted array with binary search |
Graphically putting all these together, one gets this graph:
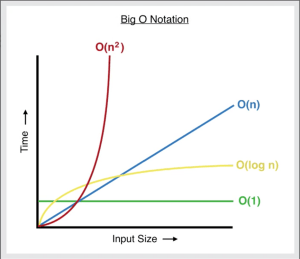
Honourable Big-O notations:
O(n log n) – Linearithmic: Sorting elements in array with merge sort
O(n3) – Cubic: 3 variables equation solver
O(2n) – Exponential: Find all subsets
O(n!) – Factorial: Find all permutations of a given set/string
Further reading:
Big-Ω notation. The difference between Big-O notation and Big-Ω notation is that Big-O describes the worst case running time for an algorithm while the Big-Ω describe the best case running time for a given algorithm.

Leave a comment